Supervisor: Dr.ir. M.A. van Huis
Promotors: Prof.dr. A. van Blaaderen and Prof.dr.ir. M. Dijkstra

Employed since November 2012
Funded by NWO

Density functional theory, Molecular dynamics simulations

In the past decade, the interest in two dimensional (2D) nanomaterials has increased dramatically, since they show many desirable physical and electronic properties, often very different from their bulk counterparts. This revolution started with graphene and now includes a large variety of materials, such as hexagonal boron nitride (h-BN), metals, metal oxides, transition metal dichalcogenides (TMDs) and semiconductors. Thicknesses of such materials can range from a single atomic layer to a few hundred nanometers, while the size in the lateral dimensions is several orders of magnitude larger. Such nanoplatelets, nanosheets or nanomembranes show great promise for applications in flexible electronics, biomedics, optoelectronics, and catalysis.
One particular system of interest are the zinc blende (ZB) cadmium selenide (CdSe) nanoplatelets synthesized in solution by Ithurria and Dubertret[1]. The thickness of these platelets is only several atomic layers and can be accurately controlled. The exposed (001) surface is atomically flat, while the lateral <100> and <010> directions can extend to roughly 100 nm, depending on the reaction time. The platelets act as 2D quantum wells and show an extremely sharp photoluminescence peak due to quantum confinement, making them a suitable candidate material for optoelectronic applications.
Currently it is not completely clear why the platelets are synthesized in the ZB crystal structure instead of the wurtzite crystal structure, the most stable CdSe polymorph. Ligands are thought to play a major role in the synthesis mechanism, although lamellar assembly is excluded. To elucidate this process we did Density Functional Theory calculations (DFT) on WZ and ZB slabs, both with and without acetate covering the surface. The results clearly show that indeed the acetate is crucial for the stability of the ZB structure. The DFT calculations were done on small systems at 0 K. To accurately describe the synthesis conditions, larger calculations must be done at elevated temperatures. As DFT calculations are unfeasible for systems of this size, we are currently doing Molecular Dynamics simulations to gain more insight into the mechanisms of the synthesis.

Figure 1: a) Dihydrogen monoxide in its solid state. b) Dihydrogen monoxide in its liquid state.

[1] S. Ithurria et al., JACS 130, 49, 16504-16505 (2008)

Stabilization of rock salt ZnO nanocrystals by low-energy surfaces and Mg additions, a first principles study

Density functional theory (DFT)

Whereas bulk zinc oxide (ZnO) exhibits the wurtzite crystal structure, nanoscale ZnO can also be synthesized in the rock salt structure by addition of Mg. Using first-principles methods, we investigate two stabilisation routes for accessing rock salt ZnO.

The first route is stabilization by Mg addition, which was investigated by considering ZnO-MgO mixed phases. Density Functional Theory (DFT) calculations show that the rock salt phase is energetically favored over the wurtzite phase for Mg concentrations x > 0.67. The bulk phase diagram, obtained by taking only ‘ideal’ mixing entropies into account, indicates that ZnO and MgO are only slightly miscible at 300 K and that in general phase separation will occur for the bulk phases. Therefore, the formation of Mg doped ZnO nanocrystals in the rock salt structure cannot be explained solely by bulk formation energies.

The second route is through size effects, as surface energies become dominant for small nanocrystal sizes. Surface energy calculations show that ZnO surfaces are always lower in energy than their MgO counterparts. This implies that MgxZn1−xO nanoparticles are ZnO terminated. Surprisingly, the ZnO rock salt (001) surface energy is lowest of all, low enough to stabilize very small pure ZnO rock salt nanoparticles (less than 1.6 nm). At finite temperature, Mg addition greatly extends the size range for which these rock salt particles are stable. At T = 0, the phase diagram shows ranges in which a core-shell particle is predicted to be the most stable configuration, although the energy differences with mixed phases are very small.

The present approach could be applied to predict the stabilization of many other nanocrystal phases in deviating crystal structures.

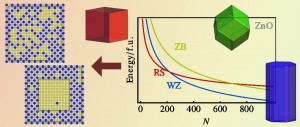
Figure 1:  For each composition and temperature, the stability of each nanoparticle as a function of its size can be determined.