Carmine Anzivino -Particles at fluid interfaces

Over a century ago it was observed that sub-millimeter sized particles adsorb at fluid interfaces and that, once adsorbed, these particles can attract each other and clump together allowing for the formation of stable 2D structures. From a qualitative point of view an adsorbed particle in general induces deformations in the shape of the fluid-fluid interface and these capillary deformations are in turn responsible for capillary interactions that are usually strong enough to induce the formation of the mentioned 2D structures. Such a self-assembly process depends strongly on the so-called contact angle, that determines the curvature of the fluid-fluid interface, and on the particle’s shape and surface chemistry. By tuning these factors it is possible to control the formation and the properties of the 2D structures.
A theory able to explain in a complete manner the self-assembly of particles at interfaces and to make quantitative predictions has not yet been elaborated. Indeed, following a pioneering study by Pieranski [1], the theoretical predictions are usually based on the assumption that the fluid-fluid interface remains flat even when the particle is adsorbed and it thus ignore the capillary deformations induced by the particle. Nevertheless a new numerical method has been recently developed that goes beyond Pieranski’s approximation and takes into account the capillary deformations [2]. By using this new method it has been possible to show that neglecting capillary effects can lead to erroneous predictions and, at the same time, it has been possible to predict self-assembly of particles in agreement with experimental observations [3]. The goal of my project is to use the new elaborated numerical method in order to obtain new theoretical predictions and a better understanding of the self-assembly of particles at fluid interfaces.

[1] P. Pieranski, Phys. Rev. Lett. 45, 569 (1980)
[2] G. Soligno, M. Dijkstra, and R. van Roij, J. Chem. Phys. 141, 244702 (2014)
[3] G. Soligno, M. Dijkstra, and R. van Roij, Phys. Rev. Lett. 116, 258001 (2016)

Emanuele Boattini – Neural network based order parameters for classification of binary crystal structures

In many types of research, such as study of crystallization from the undercooled liquid, one needs to be able to distinguish particles that are part of the crystal from those that belong to the liquid. Moreover, it is very often desirable to be able to discriminate between different crystal structures. Ideally, such an assignment should be based on the local environment of the particles only.
Several methods to extract local structural information on a single particle basis have been proposed. Given their success for single component systems, in this study we use the averaged local bond order parameters proposed by Lechner and Dellago [1]. Combinations of such bond order parameters are usually used in pairs in order to identify regions on a plane spanned by the pairs that correspond to different environments – and sometime more than one set of pairs are necessary. While specific combinations that discriminate between different, single-component, crystal structures have been identified [1] via trial and error, their binary counterparts do not yet exist. Here we focus on binary mixtures of hard spheres of various size ratios for which several crystal structures are predicted
to be stable. We develop a supervised artificial neural network to function as an order parameter that ‘learns’ to distinguish different binary crystalline and fluid environments on a single particle basis,
by analyzing vectors composed of several averaged local bond order parameters.
The training dataset for the network is produced by performing Monte Carlo (MC) simulations of the crystals under study. Once the network is trained, the classification process is computationally very cheap, so that it can easily be employed  in real-time during simulations. Figure 1 shows the classification of hard spheres in a simulation of coexistence between one of the Laves phases, MgCu₂, and an FCC crystal of large particles.

Figure 1: Neural network classification of a configuration of hard spheres displaying a coexistence of MgCu2 (brown) and FCC (orange) crystals . Blue particles represent the fluid, and are located at the disordered interface between the crystalline regions.

[1] W. Lechner and C. Dellago, J. Chem. Phys. 129, 114707 (2008)

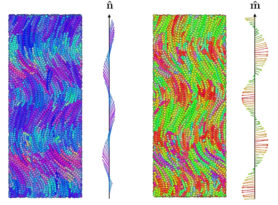
Massimiliano Chiappini – Of Twist, Bend and Other Deformations

In a seminal work of 1958, F. C. Frank introduced a continuum theory of mechanical deformations in nematic liquid crystals [1], paving the way for the physics of spontaneously deformed nematic phases.
Working on Frank’s theory, R. B. Meyer [2] and I. Dozov [3] noticed that a nematic state with a deformation of pure bend could not exist, whereas in order to homogeneously fill the space and eventually become thermodynamically stable the bend deformation has to be accompanied by either a twist or a splay deformation, postulating the existence of the so-called twist-bend and splay-bend nematic phases. Since then, many stable twist-bend nematic states have been identified and extensively characterized both in experiments and simulations. Vice versa, a stable splay-bend nematic state has not yet ever been found in experiments or simulations, the splay-bend nematic phase remaining elusive after almost 20 years.
In my research I perform computational studies of the phase behaviour of hard particles of various shape and size in order to identify the ingredients necessary for the twist- and/or splay-bend nematic phases to be stabilized. In particular, I have recently been exploring the hypothesis of particles’ curvature to be the main responsible for the formation of spontaneously deformed nematics of bent-core mesogens. From this hypothesis, a mechanism of propagation of curvature from the microscopic to the macroscopic scale can be theorized leading to interesting consequences, as the stability of the splay-bend nematic phase and the reverse engineering of the pitch of the twist-bend nematic phase. In the future I will test this hypothesis by means of an extensive computational study, in order to locate a stable splay-bend nematic phase and characterize both the twist- and the splay-bend nematic phases of bent-core mesogens.

Figure 1: A twist-bend nematic state.

[1] F.C. Frank, Discuss. Farad. Soc., 25 (1958)
[2] R.B. Meyer, in Molecular Fluids, Gordon and Breach, New York (1976), pp. 271-343
[3] I. Dozov, Europhysics Letters, 56 (2001)

Gabriele Coli – Simulations of nucleation of colloidal Laves phases

Colloidal crystals with lattice spacings similar to the wavelength of light are perfectly suitable for the manipulation of light itself. The currently known clear champion structures to realize photonic crystals are the colloidal analogues of the MgCu₂, MgZn₂ and MgNi₂ Laves phases [1]. The huge variety of potential applications, ranging from photovoltaic cells to optical computer chips, makes it fundamental to understand how to tune the parameters to favor the formation of a crystal structure with respect to another. To this aim, we investigate the nucleation process of the Laves phases by means of numerical simulation. In order to control the kinetic self-assembly process, the size, structure and rate with which a nucleus appears are crucial parameters. To probe these rare events we implement the seeding approach [2], which consists in inserting a crystal cluster of a known shape and size into a metastable fluid configuration. Keeping the temperature fixed and running the simulations for different values of the pressure we calculate the critical size of the crystal cluster which is stable at that pressure value. This information, together with other physical observables of interest – e.g. difference of chemical potential between the two phases, kinetic pre-factor of the nucleation rate and density of the metastable fluid – gives a full description of the process, including the value of the Gibbs Free Energy barrier to overcome in order to complete the transition. It is important to stress that this method strongly relies on the validity of Classical Nucleation Theory. To distinguish crystal particles from fluid particles we use bond orientational order parameters based on the computation of spherical harmonics and we then identify the nuclei using a clustering algorithm [3].

Figure 1: Crystal cluster of MgCu₂ inserted in a fluid configuration of mixture of nearly-hard spheres. The particles are coloured as follows: i) Red: Large MgCu₂-like particles ii) Orange: Small MgCu₂-like particles iii) Pink: fluid-like particles iv) Other colours: different unidentified structures.

[1] A.P. Hynninen et al., Nature Materials 6, 202-205 (2007)
[2] J. R. Espinosa et al., The Journal of Chemical Physics 144, 034501 (2016)
[3] L. Filion et al., The Journal of Chemical Physics 133, 244115 (2010)

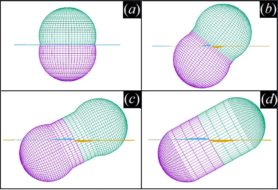
Robin van Damme – Simulations of active matter in confinement and self-assembly of anisotropic colloidal particles

Active matter is the grouping term for many-body out-of-equilibrium systems that exhibit collective behaviour (partially) as a result of energy being added to the system, usually on a local scale. These active systems come in many forms: bacterial swimming motion through the use of flagella, chemically anisotropic particles self-propelling as a result of a chemical reaction on their surface, or the biological cytoskeleton where myosin motor proteins walk over microtubuli and actin filaments, pushing them in return in accordance with Newton’s third law. For some of these systems, the interplay between their active nature and their anisotropic shape is crucial to explaining the phenomena they exhibit.

In my research I use Brownian dynamics simulations to study the collective behaviour of a collection of self-propelled rodlike particles, either in bulk or while confined to certain geometries such as a soft, deformable shell. Currently I am investigating the motility-induced phase separated (MIPS) state [1,2], and why it appears for spherical particles but not for rodlike particles.

In addition to my research on active matter, I also collaborate with experimental groups to study the self-assembly of colloidal particles of various shapes, usually through the use of Monte Carlo simulations.

Figure: (left) Self-propelled rods confined to a deformable shell. (right) Snapshot of hourglass-shaped particles self-assembling while confined to a fluid-fluid interface.

[1] M. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys. 6:1 219-244 (2015)
[2] S. Ramaswamy Annu. Rev. Condens. Matter Phys. 1:1 323-345 (2010)

Tonnishtha Dasgupta – Self-assembly of hard spheres under gravity and spherical confinement

We study the sedimentation of colloidal hard spheres using event-driven Brownian Dynamics simulations (of pure and binary mixtures) to investigate the formation of crystal phases along the sedimentation column. We obtain large single FCC crystals with very few extended defects from sedimenting pure hard spheres at high speeds on an FCC (100) template [1]. Such a crystal is shown in Figure 1. We also study binary hard spheres under sedimentation, for which case we correlate the sedimentation equilibria to the bulk thermodynamics using a theoretical construct known as a stacking diagram [2]. A stacking diagram comprises a set of all possible stacking sequences of phases formed by binary mixtures in a sedimentation column. Our aim is to obtain the stable Laves phase (a binary crystal with photonic properties), which is known to form in bulk for a diameter ratio of 0.76 to 0.84, via sedimentation.

In another line of research, we are investigating the self-assembly of binary hard spheres under spherical confinement. These simulations attempt to mimic the self-assembly of nanoparticles inside evaporating droplets of an oil-in-water emulsion into binary supraparticles [3]. However the parameter space for simulating these supraparticles is extensive and as such poses a challenging problem.

Figure 1: Large single crystal of FCC, with few extended defects, formed on deposition of pure hard spheres on the FCC (100) template at Pe = 10. Particles are coloured as follows (i) blue: fcc-like, (ii) green: fluid-like and (iii) lilac: defects.

[1] K.E. Jensen et al., Soft Matter 9, 320-328 (2013)
[2] D. Heras et al., Soft Matter 9, 8636-8641 (2013)
[3] T. Kister et al., Nanoscale 8, 13377-13384 (2016)

Guilia Fiorucci – Hydrodynamics in colloidal systems

We perform numerical simulations of colloidal particles embedded into a fluid phase of solvent particles and we analyze the behavior and the properties of this system in several physical conditions. Our aim is to investigate the dynamics of colloidal suspensions in the presence of the solvent, which is responsible for the transport of momentum throughout the system. This naturally leads to the coupling of colloidal particles, resulting as an effective interaction -hydrodynamic interactions (HI) which has many-body character. The incorporation of the HI in our model, through the Stochastic Rotation Dynamics technique [1], enable us to characterize the role of hydrodynamics in colloidal systems. We study the system composed of a dumbbell particle dragged by the fluid flow in geometrical confinement; work inspired by the experiments on a microfluidic device [2]. This simple system already exhibits a large variety of behavior which is governed by the hydrodynamic interactions of the particle with itself and with the boundaries of the channel. In our study we focus on the self-interaction of the dumbbell, which is mainly responsible for the orientation of the particle along the direction of the fluid flow. For a symmetric particle  we observe a lateral drift without any change in the orientation, however in an asymmetric particle the smaller sphere is dragged upstream, reaching the equilibrium position. At the moment we are performing several simulations at different Peclet numbers, exploring up to the region where the Brownian forces are of the same order of the hydrodynamic forces and verify up to which physical condition it is possible to have stable self-orientating phenomena.

Figure 1: a) Sketch of the system: a dumbbell particle in a channel with external flow. b) θ angle as a function of time. c) Velocity profile of solvent particles.

[1] J. T. Padding and A. A. Louis, Phys. Rev. E 74, 031402 (2006)
[2] E. Uspal et al., Nature Communications 4, (2013)

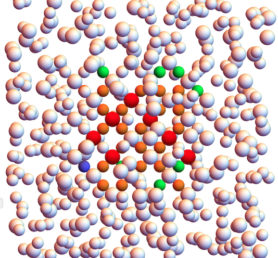
Somil Gupta – Role of magnetic defects at the water-CdS interface

Over the past decade, CdS nano-heterostructures with other semiconductors and metal co-catalysts have been developed for photocatalytic hydrogen production.^[1]

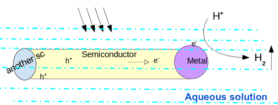
Fig. 1 shows a schematic of the currently proposed mechanism. An understanding of  the water-CdS interface is vital for elucidating the near-surface dynamics of water, and for discerning active sites for surface catalysis. To identify the key surface motifs at this interface, we study the molecular interaction of water on the clean and defected surface facets of wurtzite CdS.

The cationic vacancy defects in II-VI bulk semiconductors are known to have a net local spin, resulting from localized holes at the neighboring anions. Using spin-polarised density functional theory we study these vacancies at the most stable CdS surfaces, and study their interaction with a water molecule. We find that the magnetic moment at the cationic vacancy survives at the surface, only when neighboring S-atom relaxations are restricted by the surface geometry. At one of the more stable magnetic defect centres, we observe very strong adsorption of a water molecule. This is in agreement with experimental literature where a strong adsorption of water vapour on CdS surfaces was reported. Such a magnetic surface motif was so far not considered in simulating the water-semiconductor interfaces; our simulations indicate their relevance, and allow a comparison with electronic paramagnetic resonance experiments.

Figure 1: Schematic of the photo-catalytic splitting of water using semiconductor nano-heterostructures

[1] Chen et al., Chemical Reviews 110, 6503–6570 (2010)

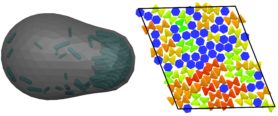
Berend van der Meer – Defects in colloidal crystals

Particles in a crystal phase are typically orders of magnitude less mobile than those in a fluid phase. Nonetheless, particles in a crystal can diffuse via the motion of defects, such as vacancies and interstitials. The motion of these defects plays an important role in the transport and mechanical properties of materials, and are a crucial factor for mechanical instabilities such as creep, yield, and fracture. Additionally, the diffusion of foreign species of particles through a crystal can be used to change its properties. However, while these defects are clearly important for material properties, little is known about the dynamics of defects in colloidal crystals.
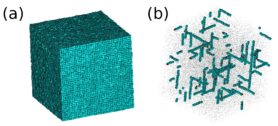
In this project, we use computer simulations to investigate defects in a range of colloidal crystals including hard cubes [1,2], hard spheres [3], binary mixtures of hard spheres [4,5], but also mixtures of active and passive particles [6,7]. These systems are ideal for this study as the defects are highly mobile. We expect our research to shed new light on defect diffusion in crystalline solids.

Figure 1: (a) Crystal of hard cubes containing many extended vacancy defects. (b) Visualization of these delocalized vacancies in the crystal. The particles that are part of the vacancy are displayed at their original size, while others are displayed much smaller.

[1] F. Smallenburg et al., PNAS 109, 17886 (2012)
[2] R. van Damme et al., JCP 147, 124501 (2017)
[3] B. van der Meer et al., JCP 146, 244905 (2017)
[4] L. Filion et al., PRL 107, 168302 (2011)
[5] B. van der Meer et al., JCP accepted (2017)
[6] B. van der Meer et al., Soft Matter 12, 3406 (2016)
[7] B. van der Meer et al., Soft Matter 12, 5630 (2016)

Siddharth Paliwal – Computational study of Self-propelled particles

Self-propelled particles belong to a class of active systems that constantly convert energy into motion, resulting in a continuous dynamic reorganization of the constituents. A fascinating variety of non-equilibrium phenomena like swarming, lane formation, giant density fluctuations, clustering, vortices, etc. has been revealed by a number of synthetic and biological systems. Theoretical models of these systems, apart from the aforementioned novelties, have also been known to show equilibrium-like phenomena such as condensation, phase transition, crystallization etc. The recent research in the field has been towards explaining such behavior in terms of modified thermodynamic quantities.

We focus on the systematic study of collective behavior of these self-propelled particles using multi-particle Brownian dynamics simulations as a function of the relevant system parameters such as density, size, shape, self-propulsion speed and interactions of the nanoparticles. We implement a model system as a colloidal fluid interacting via Lennard-Jones or a repulsive pair potential and exhibiting self-propulsion and free rotational diffusion (also known as the Active Brownian Particle model) in both two and three dimensional periodic systems. We study various thermodynamic properties such as the states of phase-coexistence, mechanical pressure, interfacial tension [1] and chemical potential. Our results indicate that even though coexisting states display mechanical and diffusive equilibrium via modified pressure and chemical potential, these properties not only depend on the bulk state but also on the interfaces in such systems [2].

Figure 1: (a) Snapshot of simulation showing phase coexistence of repulsive Active Brownian particles in 2D (color indicates local density) (b) Density (blue) and Polarization (red) profiles, and (c) Pressure-density equation of state with the inset showing a comparison of the actual coexistence densities with the predictions from a Maxwell equal area construction.

[1] V. Prymidis, S. Paliwal, M. Dijkstra, L.Filion, JCP 145, 124904 (2016)
[2] S. Paliwal, J. Rodenburg, R. v. Roij, M. Dijkstra, NJP 20, 015003  (2017)